Alig néhány perccel azután, hogy a facebook-oldalamon megosztottam ezt a grafikont, két kérdést is kaptam hozzá kapcsolódóan. A kettő közül az, amelyikre röviden tudtam válaszolni, így hangzott, idézem: „milyen állat a corn?” (megfejtés: kígyó).
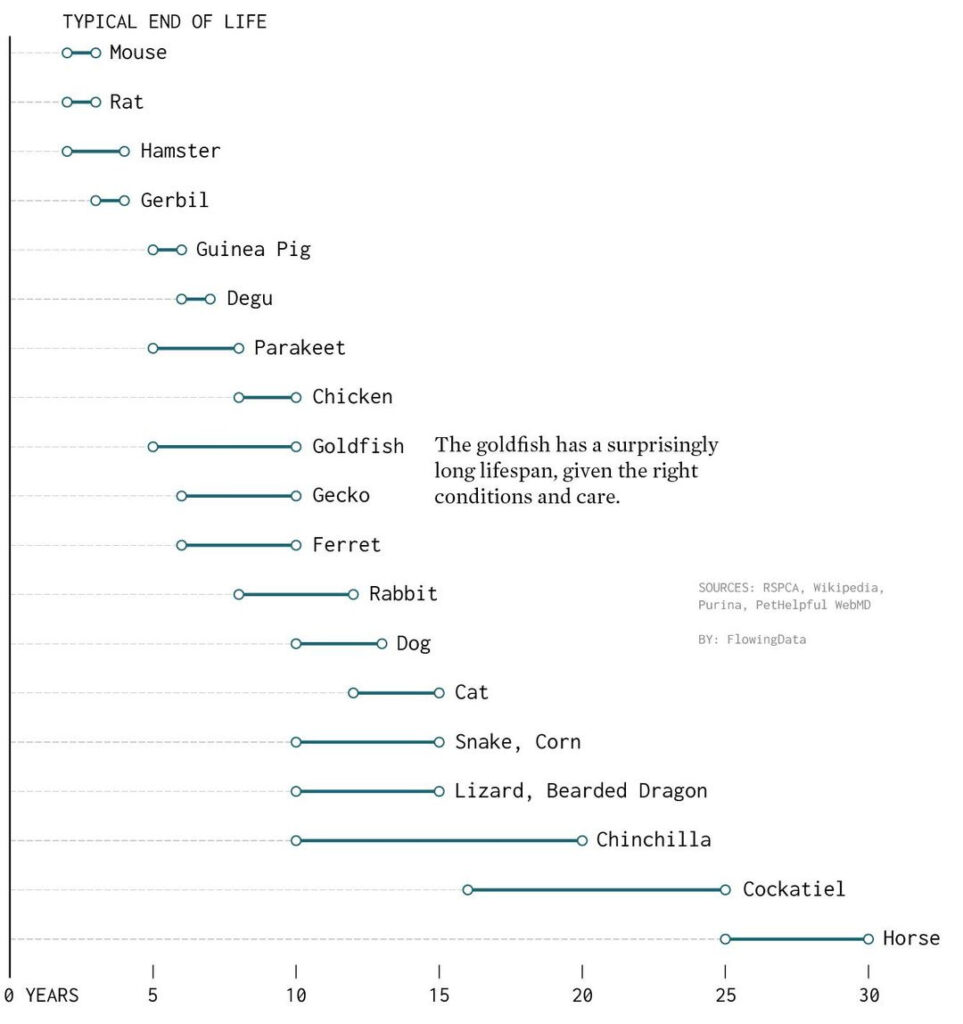
A másik viszont hosszasabb kifejtést igényel, nevezetesen hogy miért nem konkrét átlagértékeket látunk a grafikonon; vajon miért van minden állat mellett egy szakasz?
Lépjünk néhányat vissza, és nézzük meg, hogyan lehet a kérdésre válaszolni: átlagosan meddig él egy házimacska? Nyilván adatokat kell gyűjtenünk konkrét macskák élettartamáról (hogy ezt hogyan, mikor, milyen feltételekkel érdemes csinálni, most ne firtassuk); a képzeletbeli kutatásunkban ugorjunk oda, amikor van egy, mondjuk 100 adatot tartalmazó adatbázisunk macskák életéveinek számával.
Az első lépés nyilván az lesz, hogy átlagot számolunk a 100 értékből; legyen mondjuk ez 13,5 év. Ez a szám azonban csak a 100, a mintánkban szereplő cicáról mond el valamit – minket viszont általánosságban érdekelne, meddig élnek a macskák.
Ha a mintából az összes cica élettartamára következtetünk, akkor statisztikai terminológiával élve becslést végzünk. Ehhez kell némi bátorság előzetes tudás, de ha nagyon egyszerűen gondolkodunk, mondhatjuk, hogy mivel a minta átlaga 13,5; az összes cica, akire a becslés vonatkozik, átlagosan 13,5 évet fog élni. Sőt, csak egy átlag birtokában ennél sokkal jobb értéket nem is tudunk kijelölni az összes cica életkorára; hiszen indokolatlan lenne mondjuk 13, vagy 16 évet mondani, ha egyszer a minta átlaga 13,5 lett.
Viszont, hála a valószínűségszámítás és a matematikai statisztika csodálatos módszertanának, ennél azért tovább is tudunk menni. Számszerűsíteni lehet ugyanis azt, hogy bizonyos keretek között mekkora hibára lehet számítani amiatt, hogy egy mintából következtetünk egy sokkal nagyobb elemszámú, vagy éppen végtelen elemszámú sokaságra (más szóval populációra). Ezt a kalkulált hibát (tegyük fel, ez 1,5 év a példánkban) pedig arra tudjuk használni, hogy a 13,5 átlagot korrigáljuk vele. Ha kivonjuk az átlagból a hibát, majd hozzá is adjuk, egy olyan intervallumot kapunk, amiben minden cica átlagos életkora (egy bizonyos, előre meghatározott megbízhatósággal) benne van; nem pedig csak azé a százé, aki a mintába került. Egészen konkrétan ebben a példában a cicák átlagos élettartamának pontbecslése 13,5 év; intervallumbecslése pedig a 12 és 15 év közötti intervallum, jelöléssel: [12;15] – és, visszatérve a kiinduló kérdésünkre, ezt látjuk tól-ig a grafikonon.
Ha tudok a vizsgára készülésben, beadandók elkészítésében, a kutatásod megtervezésében, vagy elemzésben segíteni, vedd fel velem a kapcsolatot!
(A képen szeretett Katie cicánk, aki sajnos csak 14 évet élt.)