Az egyik legizgalmasabb statisztikai „fejtörő”, amivel tanulmányaim során találkoztam, az úgynevezett német tank probléma. A legérdekesebb benne, hogy egy teljesen valós, életbevágó helyzetben kellett jól kalkulálniuk a matematikusoknak – és, mint hamarosan kiderül, ez sikerült is nekik.
A II. világháborúban a szövetségeseknek elemi érdekük volt, hogy tudják, a németek mennyi tankot képesek gyártani – hiszen erre alapozva tudtak fontos stratégiai döntéseket hozni. (Nincs ez ma sem másként, ma is azért gyűjtünk adatokat, hogy megismerjük a valóságot; és szükség esetén változtassunk rajta.) Eleinte azt gondolták, hogy ehhez az információhoz csak hírszerzési módszerekkel lehet hozzájutni – a szövetségesek kémei szerint a németek havonta 1500 tank gyártására voltak képesek. Valakinek viszont az a zsneiális ötlete támadt, hogy talán számolni is érdemes lenne kicsit. Mi lenne, ha az ismert tankalkatrészek sorszámait használnák fel annak a becslésére, hogy összesen mennyi tank készült? Némi adat rendelkezésre állt erről ugyanis; a kilőtt, vagy ilyen-olyan módon megfigyelt tankokról leolvashatóak voltak a sorszámok – amik nyilván növekvő sorrendben követték egymást.
Matekra lefordítva ez tehát azt jelenti, hogy egy felsorolásszerű adathalmaz maximumát kell megbecsülnünk úgy, hogy a felsorolásnak csak bizonyos elemeit ismerjük. Hogyan lehet ezt kiszámolni? Az intuitívan adódó következtetés csak annyi, hogy a legnagyobb, ismert sorszámúnál magasabb a gyártott mennyiség; de vajon mennyivel? Gondolkodhatunk úgy is, hogy sorbarendezett értékeinkben, ha véletlenszerűséget feltételezünk a megtalálásukban, a legkisebb ismert érték, és a skála eleje (1.számú tank) között ugyanakkora az eltérés, mint a legnagyobb ismert érték, és a skála maximuma (az utolsó, legyártott tank sorszáma) között.
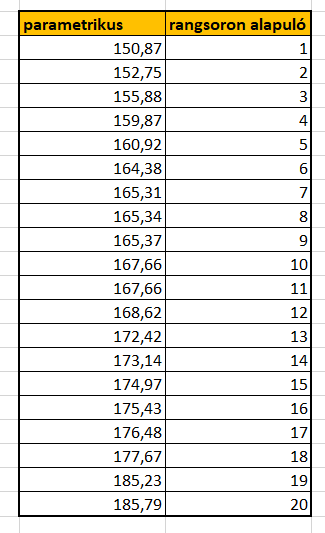
Ezzel azonban, többek között az a probléma, hogy nem használunk fel minden adatot; a közbülső sorszámok, mint információ, elvesznek. Ebből kiindulva érdemes úgy kalkulálni, hogy a maximumot egy olyan intervellum hozzáadásával növeljük, ami a megtalált sorszámok közötti eltérések átlaga, azaz a gyártott tankok száma = maximum megtalált sorszám + megtalált sorszámok közötti eltérések átlaga képlettel dolgozni. Az általam bemutatott példában a 60 a tényleges maximum, ezt próbáljuk 7 „megtalált tank” sorszámából a fenti képlettel megbecsülni.

Az eltérések a sorszámok között 5,7,12,4,15,és 6; ezek átlaga kerekítve 8,2. Ezt hozzáadva a legnagyobb megtalált sorszámhoz 61,2 az eredmény; vagyis kerekítve azt mondanánk, hogy 62 legyártott tankkal tudnak a döntéshozók kalkulálni; mindezt úgy, hogy a valós érték 60 volt.
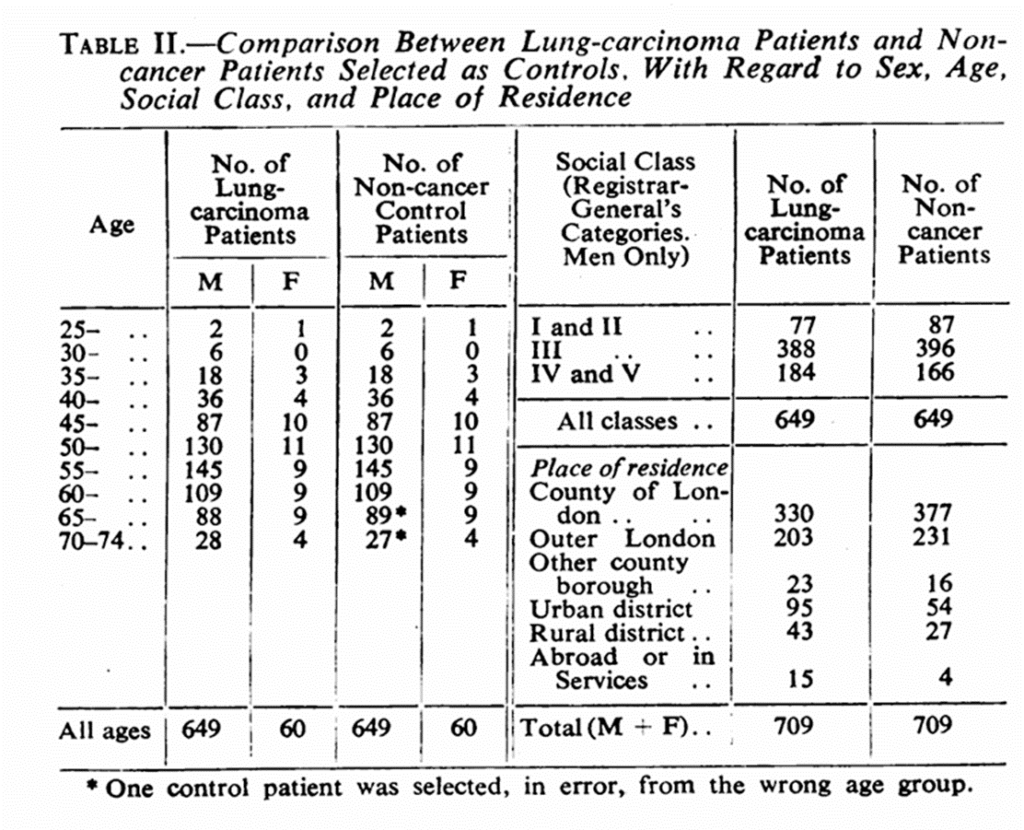
A tényleges, világháborús számítások módszertana nem ismert; tehát nem lehetünk biztosak benne, hogy a tankok számát becsülni próbáló matematikusok is ezt az átlagos különbséges képletet használták -e. Nyilvánvaló az is, hogy a valós számításokban sok olyan egyéb körülményt is figyelembe kellett venni, ami ebből a leegyszerűsített számításból most kimaradt. Az viszont biztos, hogy a matematikusok lényegesen jobban teljesítettek a terepen dolgozó kémeknél; bizonyíték erre többek között ez a táblázat. A szövetségesek győzelme után ismertté váló gyártási adatok tükrében egyértelmű, hogy a gyártási szám alapú kalkulációk nagyságrendileg kevesebb eltérét mutatnak a ténylegesen gyártott adatoktól:

forrás: https://www.tandfonline.com/doi/abs/10.1080/01621459.1947.10501915