Röviden: ami közös bennük, hogy mindkettőt két (azaz kizárólag kettő) csoport összehasonlítására használjuk. Jobban parkolnak -e a férfiak, mint a nők? A nevelőotthonban felnőtt gyerekeknek más -e a szorongásszintje, mint a családban nevelekdőkének? A 25 év alattiak többet használják -e közösségi médiát, mint a 25 év felettiek?

Míg azonban a t-teszt parametrikus (ez alatt itt azt értjük, hogy feltétele a normáleloszlás), addig a Mann-Whitney rangsoroláson alapul. Ez tulajdonképpen azt jelenti, hogy a Mann-Whitney során elvész az egymást követő adatok távolságának különbözősége, minden érték között 1 egység lesz a távolság:

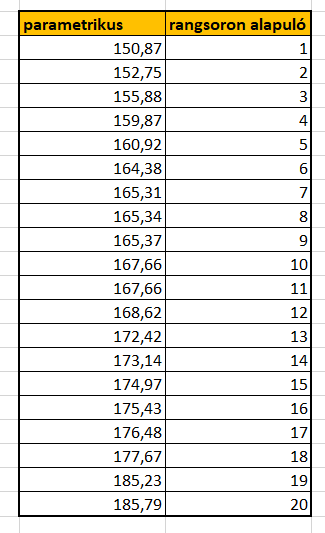
Ennek az az előnye, hogy az eloszlás normalitása itt már nem fontos; hiszen az egymás után sorban beszámozott értékekben az úgysem mutatkozna meg; de ugyanez a tulajdonsága okozza a kisebb erejét is. Az óráimon viszonylag rendszeresen felmerül a kérdés, hogy miért nem használjuk automatikusan a nemparaméteres teszteket, ha egyszer ugyanazt a funkciót töltik be, mint a paraméteresek, csak sokkal kevesebb előfeltétellel? A válasz az erőben rejlik: a nemparaméteres próbák egyszerűen kevésbé hatékonyak – ami viszont nem az elsődleges szempont akkor, amikor a normalitás sérülése miatt paraméteres próbát nem használhatunk…

A gyakorlatban úgy tudunk a kétféle teszt közül választani, hogy ha a normalitás rendben van (ellenőrizni leggyakrabban a Shapiro-Wilk teszttel szoktuk), akkor t-tesztet használunk; ha a normalitás nem teljesül, akkor viszont Mann-Whitney tesztet. Annak ellenére így van ez, hogy a szóráshomogenitásra is figyelnünk kellene közben, de a gyakorlatban a normalitás, mint feltétel, általában mindent visz.